あなたは「8次元って一体何？どうやって理解すればいいの？」と思ったことはありませんか？結論、8次元は私たちが日常で感じる3次元空間を超えた数学的・物理学的概念です。この記事を読むことで8次元の基本から最新の物理学での応用までがわかるようになりますよ。ぜひ最後まで読んでください。

1.8次元とは何か？基礎から理解する次元論の世界

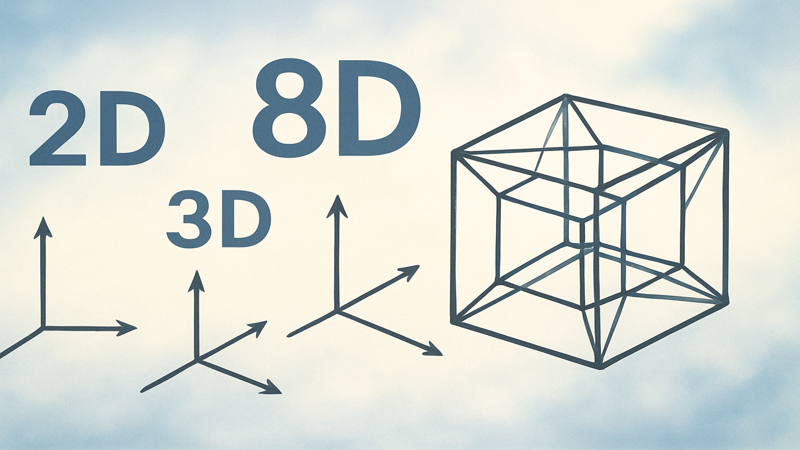
次元の基本概念と8次元の定義

次元とは、空間内の位置を特定するために必要な座標の数を表す概念です。

私たちが普段生活している世界は3次元空間（縦・横・高さ）で構成されており、これに時間を加えた4次元時空が一般的な認識です。

8次元とは、この4次元時空をさらに拡張し、8つの独立した座標軸を持つ数学的空間のことを指します。

数学的には、8次元空間の任意の点は（x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈）という8つの実数によって完全に特定できます。

このような高次元空間は、直感的に理解することは困難ですが、数学的には完全に定義可能で、様々な分野で実際に活用されています。

数学における8次元空間の特徴

8次元空間には、低次元空間では見られない独特な数学的性質があります。

まず、8次元空間では距離の概念が大幅に拡張され、2点間の距離は8つの座標成分の二乗和の平方根で表現されます。

また、8次元空間における球（超球面）の体積や表面積の計算には、ガンマ関数などの高等数学が必要になります。

線形代数の観点では、8次元ベクトル空間では最大8個の線形独立なベクトルが存在し、これらが空間全体の基底を構成します。

特に重要なのは、8次元空間では回転や対称変換が極めて複雑になり、8×8の行列による表現が必要となることです。

8次元と他の次元との関係性

8次元は、次元の階層構造において特別な位置を占めています。

低次元（1-4次元）は私たちが直感的に理解できる範囲ですが、5次元以上の高次元になると抽象的な数学的概念となります。

8次元は、物理学の超弦理論における10次元時空の一部として重要な役割を果たします。

数学的には、8次元は2の3乗であり、コンピューターサイエンスにおけるバイナリ表現との親和性が高い特徴があります。

また、8次元空間は機械学習やデータサイエンスにおいて、8つの特徴量を持つデータセットの分析空間として頻繁に利用されています。

日常生活では感じられない8次元の存在

私たちの感覚器官は3次元空間での生活に最適化されているため、8次元を直接感知することはできません。

しかし、8次元的な概念は意外にも身近な場面で活用されています。

例えば、スマートフォンの画像認識技術では、色彩、明度、コントラストなど複数の要素を8次元空間で処理している場合があります。

また、音楽制作ソフトウェアでは、音量、ピッチ、リバーブ、エコーなど8つのパラメータを同時に調整する8次元空間での作業が行われています。

現代のAI技術においても、8次元特徴空間でのパターン認識や最適化問題の解決が日常的に行われており、私たちの生活を間接的に支えています。

2.物理学における8次元の役割と超弦理論との関係

超弦理論における10次元時空と8次元空間

超弦理論は、物質の最小単位を点粒子ではなく「弦」として捉える革新的な物理理論です。

この理論では、数学的整合性を保つために10次元時空（9次元空間＋1次元時間）が必要とされています。

8次元は、この10次元時空から私たちが認識できる4次元時空を除いた「余剰次元」の大部分を構成します。

超弦理論によれば、これらの余剰次元は「コンパクト化」と呼ばれる過程で極小サイズに縮約されており、日常的なスケールでは観測できません。

8次元空間では、弦の振動パターンが複雑化し、これが素粒子の多様性を生み出す原因となっていると考えられています。

量子物理学で登場する8次元の概念

量子力学においても、8次元は重要な役割を果たしています。

量子状態の記述では、しばしば8次元ヒルベルト空間が用いられ、複雑な量子システムの状態を表現します。

特に、8個のスピン状態を持つ量子系や、8レベルのエネルギー状態を持つ原子システムの解析で8次元空間が活用されています。

量子もつれ現象の研究では、複数の粒子の状態を同時に記述するために8次元以上の高次元空間が必要になることがあります。

また、量子コンピューターの分野では、8キュービットシステムの状態空間として256次元（2^8）の空間が扱われ、この基礎として8次元概念が重要になります。

余剰次元理論における8次元の位置づけ

余剰次元理論では、私たちの宇宙に隠された高次元空間の存在が提唱されています。

カルツァ・クライン理論では、重力と電磁気力の統一を目指して5次元時空が提案されましたが、現代では8次元を含む更なる高次元が検討されています。

ADD模型（アルカーニ・ディモプロス・ドヴァリ模型）では、余剰次元の一部が8次元空間として展開している可能性が示唆されています。

これらの理論によれば、8次元空間は重力の伝播媒体として機能し、私たちが感じる重力の弱さを説明する鍵となる可能性があります。

実験物理学では、LHC（大型ハドロン衝突型加速器）などの高エネルギー実験で、8次元を含む余剰次元の証拠探しが続けられています。

重力と他の力の統一理論での8次元

現代物理学の最大の課題の一つは、重力を含む4つの基本的な力の統一理論の構築です。

大統一理論では、電磁気力、弱い核力、強い核力の統一が部分的に達成されていますが、重力を含む完全な統一には8次元以上の空間が必要と考えられています。

M理論では、11次元時空の中で8次元空間が膜（ブレーン）構造を形成し、各種の力が異なる次元で作用すると提案されています。

ホログラフィック原理によれば、8次元空間の物理現象は、その境界である7次元空間での情報で完全に記述できる可能性があります。

これらの理論的枠組みにおいて、8次元は単なる数学的概念ではなく、宇宙の根本的な構造を理解するための必須要素として位置づけられています。

3.数学的な8次元の具体例と応用分野

8次元表現とリー群理論での応用

リー群理論は、連続的な対称性を数学的に記述する強力な理論体系です。

SU(3)群（特殊ユニタリ群）の8次元表現は、素粒子物理学における強い核力の記述で中核的な役割を果たしています。

この8次元表現は、クォークとグルーオンの相互作用を支配するゲージ理論の基礎となっており、量子色力学（QCD）の数学的基盤を提供しています。

具体的には、8つのゲルマン行列が8次元空間での基底を構成し、強い核力のゲージ変換を記述します。

また、リー代数の随伴表現として現れる8次元空間は、対称性の破れや相転移現象の解析において重要な役割を果たしています。

8次元球面と多次元幾何学

8次元球面（7-球面）は、9次元ユークリッド空間に埋め込まれた7次元多様体として定義されます。

数学的には、中心からの距離が一定（通常は1）である8次元空間内の全ての点の集合として表現されます。

8次元球面の体積は π^4/24 ≈ 4.06 となり、興味深いことに7次元球面の体積（π^4/6 ≈ 16.23）よりも小さくなります。

この現象は「次元の呪い」と呼ばれる高次元空間特有の性質の一例で、直感に反する結果として知られています。

位相幾何学において、8次元球面は特殊な性質を持ち、複素数、四元数、八元数の構造と深い関連を持っています。

E8格子と例外型リー群の8次元構造

E8格子は、8次元ユークリッド空間における最も対称性の高い格子構造の一つです。

この格子は、248個の根ベクトルを持つ例外型単純リー群E8と密接な関係があります。

E8格子は、8次元空間における球充填問題の最適解を与えており、密度は約0.2537という驚くべき効率性を示します。

数論においても、E8格子は8次二次形式の極値理論や、楕円関数論との深い関連を持っています。

近年では、E8格子の対称性が、結晶学や材料科学における新しい構造設計の指針として注目を集めています。

データサイエンスにおける8次元空間の活用

現代のデータサイエンスでは、8次元特徴空間での分析が頻繁に行われています。

機械学習アルゴリズムでは、8つの入力変数を持つデータセットを8次元空間での点として扱い、パターン認識や分類問題を解決します。

具体的な応用例として、以下のような分野で8次元空間が活用されています：

• 画像認識：色相、彩度、明度、コントラスト、シャープネス、ノイズレベル、テクスチャ、形状特徴
• 音声解析：基本周波数、倍音構成、音量、継続時間、音色、発音明瞭度、背景雑音、感情指標
• 経済分析：GDP、失業率、インフレ率、金利、為替レート、株価指数、貿易収支、消費者信頼度

主成分分析（PCA）やt-SNE等の次元削減技術により、8次元データを2次元や3次元に投影して可視化することが可能です。

4.8次元を理解するための視覚化と身近な例

低次元から8次元への段階的理解法

8次元の理解には、低次元から順番に概念を積み上げていく段階的アプローチが効果的です。

まず、0次元（点）→1次元（線）→2次元（面）→3次元（立体）の流れを確実に把握します。

4次元では、3次元立体が時間軸方向に延びる概念として理解し、ハイパーキューブ（正八胞体）を例に空間的拡張を学びます。

5次元以降は、数学的な座標系として捉え、各次元を独立したパラメータと考える抽象化思考が重要になります。

8次元に到達するまでに、各段階で以下の理解ポイントを確認することが推奨されます：

• n次元空間では、n個の数値で位置を完全に特定できる
• n次元の「球」は、(n+1)次元空間に埋め込まれる
• 次元数が増加すると、体積の概念が根本的に変化する
• 高次元では、直感的理解よりも数学的定義が重要になる

コンピューターグラフィックスでの8次元表現

現代のコンピューターグラフィックス技術では、8次元データの視覚化に様々な手法が開発されています。

並行座標プロット（Parallel Coordinates Plot）では、8つの縦軸を並列に配置し、各データポイントを線で結んで8次元データを2次元画面で表現します。

レーダーチャート（Spider Chart）では、8つの軸を放射状に配置し、多角形の形状で8次元データの特徴を視覚的に把握できます。

アニメーション技術を用いて、時間軸を利用した8次元データの動的表現も可能で、各次元を時系列で順次表示する手法が開発されています。

VR（仮想現実）技術の進歩により、没入型環境での8次元データ探索が可能になり、ユーザーは仮想空間内で高次元データを直感的に操作できるようになりました。

機械学習における8次元特徴空間の実例

機械学習の分野では、8次元特徴空間での分析が実際のビジネス問題解決に活用されています。

顧客行動分析では、購入頻度、平均購入金額、サイト滞在時間、クリック数、返品率、レビュー評価、紹介数、リピート率の8指標で顧客を8次元空間にマッピングします。

医療診断支援システムでは、血圧、心拍数、体温、血糖値、白血球数、赤血球数、血小板数、CRP値の8つの検査値を用いて、疾患リスクを8次元空間で評価します。

自然言語処理では、単語の意味を8次元ベクトルで表現し、文章の感情分析や自動翻訳の精度向上に貢献しています。

これらの応用例では、8次元空間内での距離計算や類似度評価により、複雑なパターン認識問題を効率的に解決できています。

8次元思考が開く新しい科学的視点

8次元的思考は、従来の3次元的発想を超えた革新的な問題解決アプローチを提供します。

複雑系科学では、8つの異なる変数が相互作用するシステムの動態を8次元位相空間で分析し、カオス現象や創発特性の理解が深まっています。

社会科学における多変量解析では、政治、経済、文化、教育、環境、技術、人口、地理の8要素を同時に考慮した社会現象の分析が可能になります。

創造性研究では、8次元思考により、問題を多角的に捉え、従来の枠組みを超えた革新的なソリューションを発見する能力が向上すると報告されています。

未来の科学技術発展において、8次元以上の高次元思考は必須のスキルとなり、AI、量子コンピューティング、バイオテクノロジーなどの最先端分野での突破口を開く鍵となるでしょう。

まとめ

この記事を通じて、8次元に関する重要なポイントを学ぶことができました：

• 8次元は8つの独立した座標軸を持つ数学的空間概念である
• 超弦理論では10次元時空の余剰次元として8次元空間が重要な役割を果たす
• リー群理論においてSU(3)の8次元表現が素粒子物理学の基礎となっている
• E8格子は8次元空間における最も美しい対称構造の一つである
• データサイエンスでは8次元特徴空間での分析が実用的に活用されている
• 機械学習や人工知能技術で8次元データ処理が日常的に行われている
• コンピューターグラフィックス技術により8次元データの視覚化が可能になった
• 8次元思考は複雑な現実問題の解決に新しい視点を提供する

8次元という概念は決して抽象的な数学の遊びではなく、現代科学技術の最前線で実際に活用されている実用的なツールです。これからの時代、高次元思考は様々な分野での問題解決能力を飛躍的に向上させる重要なスキルとなるでしょう。ぜひこの知識を活かして、新しい発見と創造に挑戦してください。

関連サイト

• 理化学研究所（RIKEN） – 日本の代表的な基礎科学研究機関で、素粒子物理学や数学の最新研究情報を提供
• 高エネルギー加速器研究機構（KEK） – 素粒子物理学研究の中心機関で、超弦理論や次元論に関する研究成果を公開